Classics

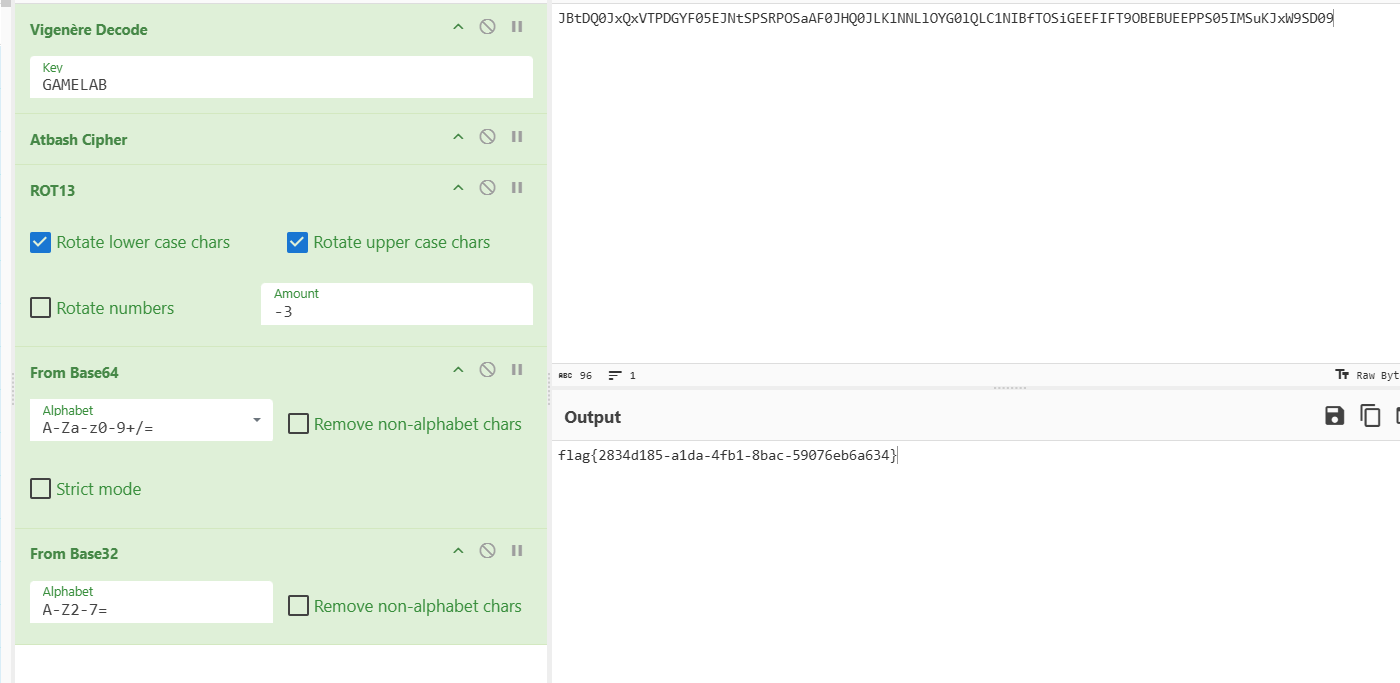
已经给出了加密方法和密文，倒着来就行

AliceAES

简单的aes，给出了key，iv和明文，直接加密


from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from Crypto.Util.number import bytes_to_long

# 密钥和初始化向量
key = b'daa0d6e430afc6af'  
iv = b'2aa3541f0ef26393'

message = 'Hello, Bob!' # 这里特别坑，最前面有个空格

# 创建 AES 加密器执行加密
cipher = AES.new(key, AES.MODE_CBC, iv)
encrypted_data = cipher.encrypt(pad(message.encode(), AES.block_size))

# 将加密结果转换为十六进制形式
print(hex(bytes_to_long(encrypted_data))[2:])

easymath

加密流程：

遍历从 $2^{l-1}$ 到 $2^l - 1$ 的所有奇数
对每个奇数 k ：
转换为二进制字符串 s = bin(k)[2:]
确保 s 中不包含连续的 1111 或 0000。
满足条件时，key 增加。
最终，key 表示符合条件的奇数个数。

p 是 k 的下一个素数，随机生成一个2048位素数 q ，然后是正常的rsa加密

解密思路

通过有限状态机和矩阵计算，统计符合特定规则的比特串总数，并由此计算密钥 key

定义状态空间
每个状态以 (last_bit, count) 表示：
last_bit 是当前比特位的值（0 或 1）。
count 是连续相同比特的个数，范围为 1 到 3。
状态集合 states 定义为：
[(0, 1), (0, 2), (0, 3), (1, 1), (1, 2), (1, 3)]
共 6 种状态。
构造状态转移矩阵
状态转移的规则：
新比特 new_bit 可以为 0 或 1。
如果 new_bit == last_bit，count 增加 1。
如果 new_bit != last_bit，count 重置为 1。
如果 count >= 4，该状态无效，不记录到转移矩阵中。

转移矩阵 T：
矩阵的元素 $T[i][j]$ 表示从状态 j 转移到状态 i 的路径数。

矩阵快速幂计算
转移矩阵 T 的 (l−1) 次幂 T^(l-1)：
表示在 l−1 步内，从任意状态到达任意状态的路径总数。
使用矩阵快速幂算法，时间复杂度 $O(log(l)⋅n^3)$
初始化状态向量
初始状态设定为 (1, 1)，即以比特 1 开头，连续相同比特计数为 1。
对应的初始状态向量为：
[0, 0, 0, 1, 0, 0]
只有状态 (1, 1) 的路径数为 1，其余为 0。
计算最终状态向量
将初始状态向量与 T^(l-1) 相乘，得到最终状态向量 final_state：
final_state[i] 表示在 l−1 步后到达状态 i 的所有路径数。
统计目标路径总数

exp

from Crypto.Util.number import *
from gmpy2 import next_prime

n=739243847275389709472067387827484120222494013590074140985399787562594529286597003777105115865446795908819036678700460141950875653695331369163361757157565377531721748744087900881582744902312177979298217791686598853486325684322963787498115587802274229739619528838187967527241366076438154697056550549800691528794136318856475884632511630403822825738299776018390079577728412776535367041632122565639036104271672497418509514781304810585503673226324238396489752427801699815592314894581630994590796084123504542794857800330419850716997654738103615725794629029775421170515512063019994761051891597378859698320651083189969905297963140966329378723373071590797203169830069428503544761584694131795243115146000564792100471259594488081571644541077283644666700962953460073953965250264401973080467760912924607461783312953419038084626809675807995463244073984979942740289741147504741715039830341488696960977502423702097709564068478477284161645957293908613935974036643029971491102157321238525596348807395784120585247899369773609341654908807803007460425271832839341595078200327677265778582728994058920387721181708105894076110057858324994417035004076234418186156340413169154344814582980205732305163274822509982340820301144418789572738830713925750250925049059
c=229043746793674889024653533006701296308351926745769842802636384094759379740300534278302123222014817911580006421847607123049816103885365851535481716236688330600113899345346872012870482410945158758991441294885546642304012025685141746649427132063040233448959783730507539964445711789203948478927754968414484217451929590364252823034436736148936707526491427134910817676292865910899256335978084133885301776638189969716684447886272526371596438362601308765248327164568010211340540749408337495125393161427493827866434814073414211359223724290251545324578501542643767456072748245099538268121741616645942503700796441269556575769250208333551820150640236503765376932896479238435739865805059908532831741588166990610406781319538995712584992928490839557809170189205452152534029118700150959965267557712569942462430810977059565077290952031751528357957124339169562549386600024298334407498257172578971559253328179357443841427429904013090062097483222125930742322794450873759719977981171221926439985786944884991660612824458339473263174969955453188212116242701330480313264281033623774772556593174438510101491596667187356827935296256470338269472769781778576964130967761897357847487612475534606977433259616857569013270917400687539344772924214733633652812119743
e=65537

# 定义状态转移规则
states = [(0, 1), (0, 2), (0, 3), (1, 1), (1, 2), (1, 3)]
state_idx = {state: idx for idx, state in enumerate(states)}
idx_state = {idx: state for idx, state in enumerate(states)}
size = len(states)

# 初始化状态转移矩阵 T
T = [[0] * size for _ in range(size)]
for idx_from, (last_bit, count) in enumerate(states):
    for new_bit in [0, 1]:
        if new_bit == last_bit:
            new_count = count + 1
        else:
            new_count = 1
        if new_count >= 4:  
            continue
        idx_to = state_idx[(new_bit, new_count)]
        T[idx_to][idx_from] += 1

def mat_pow(mat, power):
    result = [[1 if i == j else 0 for j in range(size)] for i in range(size)]  # 单位矩阵
    while power > 0:
        if power % 2 == 1:
            result = mat_mul(mat, result)
        mat = mat_mul(mat, mat)
        power //= 2
    return result

def mat_mul(a, b):
    result = [[0] * size for _ in range(size)]
    for i in range(size):
        for j in range(size):
            for k in range(size):
                result[i][j] += a[i][k] * b[k][j]
    return result

def calculate_key(l):
    # 初始状态向量
    initial_state = [0] * size
    initial_state[state_idx[(1, 1)]] = 1  # 初始状态为 (1, 1)

    # 快速幂计算 T^(l-1)
    T_pow = mat_pow(T, l - 1)

    # 计算最终状态
    final_state = [sum(T_pow[i][j] * initial_state[j] for j in range(size)) for i in range(size)]

    # 统计所有以 last_bit == 1 结束的状态路径
    key = sum(final_state[state_idx[(1, count)]] for count in range(1, 4))
    return key

# 输入长度 l，计算密钥
l = 2331
key = calculate_key(l)
print("key =", key)

p = next_prime(key)
q = n // p
phi = (p-1)*(q-1)
d = inverse(e, phi)
m = pow(c, d, n)
print(long_to_bytes(m))